Main Page   Class Hierarchy   Alphabetical List   Data Structures   File List   Data Fields   Globals  

genhexkins.c File Reference

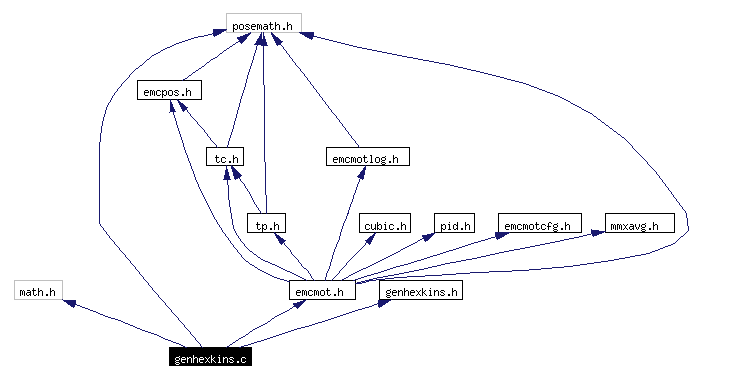
#include <math.h>
#include "posemath.h"
#include "genhexkins.h"
#include "emcmot.h"

Include dependency graph for genhexkins.c:

Include dependency graph

Go to the source code of this file.

Defines

#define HIGH_CONV_CRITERION   (1e-12)
#define MEDIUM_CONV_CRITERION   (1e-5)
#define LOW_CONV_CRITERION   (1e-3)
#define MEDIUM_CONV_ITERATIONS   50
#define LOW_CONV_ITERATIONS   100
#define FAIL_CONV_ITERATIONS   150
#define LARGE_CONV_ERROR   10000

Functions

int MatInvert (double J[][NUM_STRUTS], double InvJ[][NUM_STRUTS])
void MatMult (double J[][6], const double x[], double Ans[])
int genhexSetParams (const PmCartesian base[], const PmCartesian platform[])
int genhexGetParams (PmCartesian base[], PmCartesian platform[])
int JInvMat (const EmcPose *pos, double InverseJacobian[][NUM_STRUTS])
int jacobianInverse (const EmcPose *pos, const EmcPose *vel, const double *joints, double *jointvels)
int jacobianForward (const double *joints, const double *jointvels, const EmcPose *pos, EmcPose *vel)
int kinematicsForward (const double *joints, EmcPose *pos, const KINEMATICS_FORWARD_FLAGS *fflags, KINEMATICS_INVERSE_FLAGS *iflags)
int kinematicsInverse (const EmcPose *pos, double *joints, const KINEMATICS_INVERSE_FLAGS *iflags, KINEMATICS_FORWARD_FLAGS *fflags)
int kinematicsHome (EmcPose *world, double *joint, KINEMATICS_FORWARD_FLAGS *fflags, KINEMATICS_INVERSE_FLAGS *iflags)
KINEMATICS_TYPE kinematicsType ()

Variables

PmCartesian b [6]
PmCartesian a [6]

Define Documentation

#define FAIL_CONV_ITERATIONS   150
 

#define HIGH_CONV_CRITERION   (1e-12)
 

#define LARGE_CONV_ERROR   10000
 

#define LOW_CONV_CRITERION   (1e-3)
 

#define LOW_CONV_ITERATIONS   100
 

#define MEDIUM_CONV_CRITERION   (1e-5)
 

#define MEDIUM_CONV_ITERATIONS   50
 

Function Documentation

int JInvMat (  const EmcPose *    pos,
double    InverseJacobian[][NUM_STRUTS]
)  [static]
 

Definition at line 201 of file genhexkins.c.

Referenced by jacobianForward(), and jacobianInverse(). 

00203 {
00204   int i;
00205   PmRpy rpy;
00206   PmRotationMatrix RMatrix;
00207   PmCartesian aw, RMatrix_a;
00208   PmCartesian InvKinStrutVect,InvKinStrutVectUnit;
00209   PmCartesian RMatrix_a_cross_Strut;
00210 
00211   /* assign a, b, c to roll, pitch, yaw angles and convert to rot matrix */
00212   rpy.r = pos->a * PM_PI / 180.0;
00213   rpy.p = pos->b * PM_PI / 180.0;
00214   rpy.y = pos->c * PM_PI / 180.0;
00215   pmRpyMatConvert(rpy, &RMatrix);
00216 
00217   /* Enter for loop to build Inverse Jacobian */
00218   for (i = 0; i < NUM_STRUTS; i++) {
00219     /* run part of inverse kins to get strut vectors */
00220     pmMatCartMult(RMatrix, a[i], &RMatrix_a);
00221     pmCartCartAdd(pos->tran, RMatrix_a, &aw);
00222     pmCartCartSub(aw, b[i], &InvKinStrutVect);
00223 
00224     /* Determine RMatrix_a_cross_strut */
00225     if (0 != pmCartUnit(InvKinStrutVect, &InvKinStrutVectUnit)) {
00226       return -1;
00227     }
00228     pmCartCartCross(RMatrix_a, InvKinStrutVectUnit, &RMatrix_a_cross_Strut);
00229 
00230     /* Build Inverse Jacobian Matrix */
00231     InverseJacobian[i][0] = InvKinStrutVectUnit.x;
00232     InverseJacobian[i][1] = InvKinStrutVectUnit.y;
00233     InverseJacobian[i][2] = InvKinStrutVectUnit.z;
00234     InverseJacobian[i][3] = RMatrix_a_cross_Strut.x;
00235     InverseJacobian[i][4] = RMatrix_a_cross_Strut.y;
00236     InverseJacobian[i][5] = RMatrix_a_cross_Strut.z;
00237   }
00238 
00239   return 0;
00240 }

int MatInvert (  double    J[][NUM_STRUTS],
double    InvJ[][NUM_STRUTS]
)  [static]
 

Definition at line 65 of file genhexkins.c.

Referenced by jacobianForward(), and kinematicsForward(). 

00066 {
00067   double JAug[NUM_STRUTS][12], m, temp;
00068   int j, k, n;
00069 
00070   /* This function determines the inverse of a 6x6 matrix using
00071      Gauss-Jordan elimination */
00072 
00073   /* Augment the Identity matrix to the Jacobian matrix */
00074 
00075   for (j=0; j<=5; ++j){
00076     for (k=0; k<=5; ++k){     /* Assign J matrix to first 6 columns of AugJ */
00077       JAug[j][k] = J[j][k];
00078     }
00079     for(k=6; k<=11; ++k){    /* Assign I matrix to last six columns of AugJ */
00080       if (k-6 == j){
00081         JAug[j][k]=1;
00082       }
00083       else{
00084         JAug[j][k]=0;
00085       }
00086     }
00087   }
00088 
00089   /* Perform Gauss elimination */
00090   for (k=0; k<=4; ++k){               /* Pivot        */
00091     if ((JAug[k][k]< 0.01) && (JAug[k][k] > -0.01)){
00092       for (j=k+1;j<=5; ++j){
00093         if ((JAug[j][k]>0.01) || (JAug[j][k]<-0.01)){
00094           for (n=0; n<=11;++n){
00095             temp = JAug[k][n];
00096             JAug[k][n] = JAug[j][n];
00097             JAug[j][n] = temp;
00098           }
00099           break;
00100         }
00101       }
00102     }
00103     for (j=k+1; j<=5; ++j){            /* Pivot */
00104       m = -JAug[j][k] / JAug[k][k];
00105       for (n=0; n<=11; ++n){
00106         JAug[j][n]=JAug[j][n] + m*JAug[k][n];   /* (Row j) + m * (Row k) */
00107         if ((JAug[j][n] < 0.000001) && (JAug[j][n] > -0.000001)){
00108           JAug[j][n] = 0;
00109         }
00110       }
00111     }
00112   }
00113 
00114   /* Normalization of Diagonal Terms */
00115   for (j=0; j<=5; ++j){
00116     m=1/JAug[j][j];
00117     for(k=0; k<=11; ++k){
00118       JAug[j][k] = m * JAug[j][k];
00119     }
00120   }
00121 
00122   /* Perform Gauss Jordan Steps */
00123   for (k=5; k>=0; --k){
00124     for(j=k-1; j>=0; --j){
00125       m = -JAug[j][k]/JAug[k][k];
00126       for (n=0; n<=11; ++n){
00127         JAug[j][n] = JAug[j][n] + m * JAug[k][n];
00128       }
00129     }
00130   }
00131 
00132   /* Assign last 6 columns of JAug to InvJ */
00133   for (j=0; j<=5; ++j){
00134     for (k=0; k<=5; ++k){
00135       InvJ[j][k] = JAug[j][k+6];
00136 
00137     }
00138   }
00139 
00140   return 0;                     /* FIXME-- check divisors for 0 above */
00141 }

void MatMult (  double    J[][6],
const double    x[],
double    Ans[]
)  [static]
 

Definition at line 149 of file genhexkins.c.

Referenced by jacobianForward(), jacobianInverse(), and kinematicsForward(). 

00150 {
00151   int j, k;
00152   for (j=0; j<=5; ++j){
00153     Ans[j] = 0;
00154     for (k=0; k<=5; ++k){
00155       Ans[j] = J[j][k]*x[k]+Ans[j];
00156     }
00157   }
00158 }

int genhexGetParams (  PmCartesian    base[],
PmCartesian    platform[]
) 
 

Definition at line 187 of file genhexkins.c.

00188 {
00189   int t;
00190 
00191   for (t = 0; t < 6; t++) {
00192     base[t] = b[t];
00193     platform[t] = b[t];
00194   }
00195 
00196   return 0;
00197 }

int genhexSetParams (  const PmCartesian    base[],
const PmCartesian    platform[]
) 
 

Definition at line 175 of file genhexkins.c.

00176 {
00177   int t;
00178 
00179   for (t = 0; t < 6; t++) {
00180     b[t] = base[t];
00181     a[t] = platform[t];
00182   }
00183 
00184   return 0;
00185 }

int jacobianForward (  const double *    joints,
const double *    jointvels,
const EmcPose *    pos,
EmcPose *    vel
) 
 

Definition at line 270 of file genhexkins.c.

00274 {
00275   double InverseJacobian[NUM_STRUTS][NUM_STRUTS];
00276   double Jacobian[NUM_STRUTS][NUM_STRUTS];
00277   double velmatrix[6];
00278 
00279   if (0 != JInvMat(pos, InverseJacobian)) {
00280     return -1;
00281   }
00282   if (0 != MatInvert(InverseJacobian, Jacobian)) {
00283     return -1;
00284   }
00285 
00286   /* Multiply J[] by jointvels to get vels */
00287   MatMult(Jacobian, jointvels, velmatrix);
00288   vel->tran.x = velmatrix[0];
00289   vel->tran.y = velmatrix[1];
00290   vel->tran.z = velmatrix[2];
00291   vel->a = velmatrix[3];
00292   vel->b = velmatrix[4];
00293   vel->c = velmatrix[5];
00294 
00295   return 0;
00296 }

int jacobianInverse (  const EmcPose *    pos,
const EmcPose *    vel,
const double *    joints,
double *    jointvels
) 
 

Definition at line 242 of file genhexkins.c.

00246 {
00247   double InverseJacobian[NUM_STRUTS][NUM_STRUTS];
00248   double velmatrix[6];
00249 
00250   if (0 != JInvMat(pos, InverseJacobian)) {
00251     return -1;
00252   }
00253 
00254   /* Multiply Jinv[] by vel[] to get jointvels */
00255   velmatrix[0] = vel->tran.x;   /* dx/dt */
00256   velmatrix[1] = vel->tran.y;   /* dy/dt */
00257   velmatrix[2] = vel->tran.z;   /* dz/dt */
00258   velmatrix[3] = vel->a;        /* droll/dt */
00259   velmatrix[4] = vel->b;        /* dpitch/dt */
00260   velmatrix[5] = vel->c;        /* dyaw/dt */
00261   MatMult(InverseJacobian, velmatrix, jointvels);
00262 
00263   return 0;
00264 }

int kinematicsForward (  const double *    joint,
EmcPose *    world,
const KINEMATICS_FORWARD_FLAGS *    fflags,
KINEMATICS_INVERSE_FLAGS *    iflags
) 
 

Definition at line 304 of file genhexkins.c.

00308 {
00309   PmCartesian aw;
00310   PmCartesian InvKinStrutVect,InvKinStrutVectUnit;
00311   PmCartesian q_trans, RMatrix_a, RMatrix_a_cross_Strut;
00312 
00313   double Jacobian[NUM_STRUTS][NUM_STRUTS];
00314   double InverseJacobian[NUM_STRUTS][NUM_STRUTS];
00315   double InvKinStrutLength, StrutLengthDiff[NUM_STRUTS];
00316   double delta[NUM_STRUTS];
00317   double conv_err = 1.0;
00318 
00319   PmRotationMatrix RMatrix;
00320   PmRpy q_RPY;
00321 
00322   int iterate = 1;
00323   int i;
00324   int iteration = 0;
00325   int retval = 0;
00326 
00327 #define HIGH_CONV_CRITERION   (1e-12)
00328 #define MEDIUM_CONV_CRITERION (1e-5)
00329 #define LOW_CONV_CRITERION    (1e-3)
00330 #define MEDIUM_CONV_ITERATIONS  50
00331 #define LOW_CONV_ITERATIONS    100
00332 #define FAIL_CONV_ITERATIONS   150
00333 #define LARGE_CONV_ERROR 10000
00334   double conv_criterion = HIGH_CONV_CRITERION;
00335 
00336   /* abort on obvious problems, like joints <= 0 */
00337   /* FIXME-- should check against triangle inequality, so that joints
00338      are never too short to span shared base and platform sides */
00339   if (joints[0] <= 0.0 ||
00340       joints[1] <= 0.0 ||
00341       joints[2] <= 0.0 ||
00342       joints[3] <= 0.0 ||
00343       joints[4] <= 0.0 ||
00344       joints[5] <= 0.0) {
00345     return -1;
00346   }
00347 
00348   /* assign a,b,c to roll, pitch, yaw angles */
00349   q_RPY.r = pos->a * PM_PI / 180.0;
00350   q_RPY.p = pos->b * PM_PI / 180.0;
00351   q_RPY.y = pos->c * PM_PI / 180.0;
00352 
00353   /* Assign translation values in pos to q_trans */
00354   q_trans.x = pos->tran.x;
00355   q_trans.y = pos->tran.y;
00356   q_trans.z = pos->tran.z;
00357 
00358   /* Enter Newton-Raphson iterative method   */
00359   while (iterate) {
00360     /* check for large error and return error flag if no convergence */
00361     if ((conv_err > +LARGE_CONV_ERROR) || 
00362         (conv_err < -LARGE_CONV_ERROR)) {
00363       /* we can't converge */
00364       return -2;
00365     };
00366 
00367     iteration++;
00368 
00369 #if 0
00370     /* if forward kinematics are having a difficult time converging
00371        ease the restrictions on the convergence criterion */
00372     if (iteration == MEDIUM_CONV_ITERATIONS) {
00373       conv_criterion = MEDIUM_CONV_CRITERION;
00374       retval = -3;              /* this means if we eventually converge,
00375                                  the result is sloppy */
00376     }
00377 
00378     if (iteration == LOW_CONV_ITERATIONS) {
00379       conv_criterion = LOW_CONV_CRITERION;
00380       retval = -4;              /* this means if we eventually converge,
00381                                  the result is even sloppier */
00382     }
00383 #endif
00384 
00385     /* check iteration to see if the kinematics can reach the
00386        convergence criterion and return error flag if it can't */
00387     if (iteration > FAIL_CONV_ITERATIONS) {
00388       /* we can't converge */
00389       return -5;
00390     }
00391 
00392     /* Convert q_RPY to Rotation Matrix */
00393     pmRpyMatConvert(q_RPY, &RMatrix);
00394 
00395     /* compute StrutLengthDiff[] by running inverse kins on Cartesian
00396      estimate to get joint estimate, subtract joints to get joint deltas,
00397      and compute inv J while we're at it */
00398     for (i = 0; i < NUM_STRUTS; i++) {
00399       pmMatCartMult(RMatrix, a[i], &RMatrix_a);
00400       pmCartCartAdd(q_trans, RMatrix_a, &aw);
00401       pmCartCartSub(aw,b[i], &InvKinStrutVect);
00402       if (0 != pmCartUnit(InvKinStrutVect, &InvKinStrutVectUnit)) {
00403         return -1;
00404       }
00405       pmCartMag(InvKinStrutVect, &InvKinStrutLength);
00406       StrutLengthDiff[i] = InvKinStrutLength - joints[i];
00407 
00408       /* Determine RMatrix_a_cross_strut */
00409       pmCartCartCross(RMatrix_a, InvKinStrutVectUnit, &RMatrix_a_cross_Strut);
00410 
00411       /* Build Inverse Jacobian Matrix */
00412       InverseJacobian[i][0] = InvKinStrutVectUnit.x;
00413       InverseJacobian[i][1] = InvKinStrutVectUnit.y;
00414       InverseJacobian[i][2] = InvKinStrutVectUnit.z;
00415       InverseJacobian[i][3] = RMatrix_a_cross_Strut.x;
00416       InverseJacobian[i][4] = RMatrix_a_cross_Strut.y;
00417       InverseJacobian[i][5] = RMatrix_a_cross_Strut.z;
00418     }
00419 
00420     /* invert Inverse Jacobian */
00421     MatInvert(InverseJacobian, Jacobian);
00422 
00423     /* multiply Jacobian by LegLengthDiff */
00424     MatMult(Jacobian, StrutLengthDiff, delta);
00425 
00426     /* subtract delta from last iterations pos values */
00427     q_trans.x -= delta[0];
00428     q_trans.y -= delta[1];
00429     q_trans.z -= delta[2];
00430     q_RPY.r   -= delta[3];
00431     q_RPY.p   -= delta[4];
00432     q_RPY.y   -= delta[5];
00433 
00434     /* determine value of conv_error (used to determine if no convergence) */
00435     conv_err = 0.0;
00436     for (i = 0; i < NUM_STRUTS; i++) {
00437       conv_err += fabs(StrutLengthDiff[i]);
00438     }
00439 
00440     /* enter loop to determine if a strut needs another iteration */
00441     iterate = 0;                        /*assume iteration is done */
00442     for (i = 0; i < NUM_STRUTS; i++) {
00443       if (fabs(StrutLengthDiff[i]) > conv_criterion) {
00444         iterate = 1;
00445       }
00446     }
00447   } /* exit Newton-Raphson Iterative loop */
00448 
00449   /* assign r,p,w to a,b,c */
00450   pos->a = q_RPY.r * 180.0 / PM_PI;  
00451   pos->b = q_RPY.p * 180.0 / PM_PI;  
00452   pos->c = q_RPY.y * 180.0 / PM_PI;
00453   
00454   /* assign q_trans to pos */
00455   pos->tran.x = q_trans.x;
00456   pos->tran.y = q_trans.y;
00457   pos->tran.z = q_trans.z;
00458 
00459   return retval;
00460 }

int kinematicsHome (  EmcPose *    world,
double *    joint,
KINEMATICS_FORWARD_FLAGS *    fflags,
KINEMATICS_INVERSE_FLAGS *    iflags
) 
 

Definition at line 500 of file genhexkins.c.

00504 {
00505   *fflags = 0;
00506   *iflags = 0;
00507 
00508   return kinematicsInverse(world, joint, iflags, fflags);
00509 }

int kinematicsInverse (  const EmcPose *    pos,
double *    joints,
const KINEMATICS_INVERSE_FLAGS *    iflags,
KINEMATICS_FORWARD_FLAGS *    fflags
) 
 

Definition at line 464 of file genhexkins.c.

00468 {
00469   PmCartesian aw, temp;
00470   PmRotationMatrix RMatrix;
00471   PmRpy rpy;
00472   int i;
00473 
00474   /* define Rotation Matrix */
00475   rpy.r = pos->a * PM_PI / 180.0;
00476   rpy.p = pos->b * PM_PI / 180.0;
00477   rpy.y = pos->c * PM_PI / 180.0;
00478   pmRpyMatConvert(rpy, &RMatrix);
00479 
00480   /* enter for loop to calculate joints (strut lengths) */
00481   for (i = 0; i < NUM_STRUTS; i++) {
00482     /* convert location of platform strut end from platform
00483        to world coordinates */
00484     pmMatCartMult(RMatrix, a[i], &temp);
00485     pmCartCartAdd(pos->tran, temp, &aw);
00486 
00487     /* define strut lengths */
00488     pmCartCartSub(aw, b[i], &temp);
00489     pmCartMag(temp, &joints[i]);
00490   }
00491 
00492   return 0;
00493 }

KINEMATICS_TYPE kinematicsType (  void    ) 
 

Definition at line 511 of file genhexkins.c.

00512 {
00513 #if 1
00514   return KINEMATICS_BOTH;
00515 #else
00516   return KINEMATICS_INVERSE_ONLY;
00517 #endif
00518 }

Variable Documentation

PmCartesian a[6] [static]
 

Initial value:

 {{PLATFORM_0_X, PLATFORM_0_Y, PLATFORM_0_Z},
                           {PLATFORM_1_X, PLATFORM_1_Y, PLATFORM_1_Z},
                           {PLATFORM_2_X, PLATFORM_2_Y, PLATFORM_2_Z},
                           {PLATFORM_3_X, PLATFORM_3_Y, PLATFORM_3_Z},
                           {PLATFORM_4_X, PLATFORM_4_Y, PLATFORM_4_Z},
                           {PLATFORM_5_X, PLATFORM_5_Y, PLATFORM_5_Z}}

Definition at line 168 of file genhexkins.c.

PmCartesian b[6] [static]
 

Initial value:

 {{BASE_0_X, BASE_0_Y, BASE_0_Z},
                           {BASE_1_X, BASE_1_Y, BASE_1_Z},
                           {BASE_2_X, BASE_2_Y, BASE_2_Z},
                           {BASE_3_X, BASE_3_Y, BASE_3_Z},
                           {BASE_4_X, BASE_4_Y, BASE_4_Z},
                           {BASE_5_X, BASE_5_Y, BASE_5_Z}}

Definition at line 161 of file genhexkins.c.

Generated on Sun Dec 2 15:28:04 2001 for EMC by doxygen1.2.11.1 written by Dimitri van Heesch, © 1997-2001