Building The Big Stuff

Monster products are large items that are not easily moved. They often require hundreds, thousands or tens-of-thousands of skilled labor hours. They usually have high variety and low volume, often "one-off" designs.

Such large monster products present several unique challenges vis-a-vis the usual manufacturing situation. The most obvious challenge is material handling but there are other issues as well. These other factors are minor considerations for most products but loom large when the product itself is large.

We have had several projects involving these monster products and this series of articles derives directly from that experience. These projects included the following products:

Delivery performance is usually critical when building these large products. Fast delivery is often an important factor in winning the original order and thereby growing the business. In some industries, lead time is not important but on-time delivery (delivery reliability) is critical. For example, a delivery delay might delay the completion of a billion-dollar nuclear plant and that delay might cost millions of dollars per week.

 Fast throughput times are critical for delivery speed and usually more predictable, thus contributing to delivery reliability. Average throughput time is proportional to WIP inventory according to Little's Law. Thus reducing inventory on the shop floor leads to faster throughput which leads to faster delivery performance which leads to more reliable delivery performance.

Job#1 Principle

As a general principle, manufacturers should maximize the resources on each job even if other jobs are forced to stay in a queue. In other words, work on a few jobs simultaneously and speed them through production rather than starting many jobs and spreading resources. This is contrary to the way that most monster-product manufactuers operate but it actually results in the lowest average throughput time. There may be other advantages to this scheduling strategy which we will discuss later.

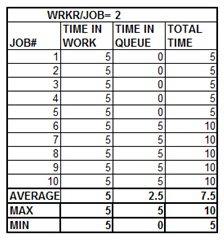
Figure 2--Average Throughput for 2 men per Job

Illustrating The Job#1 Principal

As an example, consider the hypothetical case of Figure 1. The products are large pressure vessels but this is only for visualization purposes. The Job#1 principal applies to most monster-products.  

Assume the company has firm orders for ten units and material is availible for all ten units. Ten workers are available. Each job requires 400 labor-hours. Therefore, it requires ten weeks to complete a unit with one worker or five weeks to complete the same unit with two workers or one week to complete a unit with ten workers.

The question is "what is the optimum number of workers to assign to each job." This also determines the number of jobs in progress at any given time. For the moment, we will ignore inefficiencies that may result from too many people interfering with each other's work.

Figure 2 summarizes the results for two workers per job. With two people per job, units 1-5 are in work simultaneously for five weeks and all are delivered after five weeks. Jobs 5-10 must wait while the previous five jobs are worked. They are in queue for five weeks and are in work for five weeks. The throughput time for jobs 5-10 is ten weeks. But, the first five jobs have a throughput of only five weeks. The average for all ten jobs is 7.5 weeks.

Figure 3 shows how throughput time varies as the worker allocation. Working on ten jobs simultaneously with one person per job means that every job will take ten weeks. If all ten people are put on one job, the average time drops to 5.5 weeks and only one of the jobs requires ten weeks.

Benefits of Concentrating Resources

Decreasing the average throughput time is only one of many benefits from concentrating maximum resources on the next job in line. Subsequent pages will discuss the advantages in:

Of course, practical circumstances may limit the number of people that can be usefully employed at one time. In this example suppose that only five workers can be used effectively. In that situation, the throughput time is still reduced to six weeks from ten weeks. Future articles will identify some methods that can mitigate the problem of too many people interfering with each other's work. We will also discuss the implications for plant layout, workflow and cash flow.